莫队算法

螃蟹的舞蹈。

莫队算法得名于 2010 年国家集训队队员莫涛。由于经常打比赛做队长，大家都叫他莫队。从对一个算法如此草率的命名中，可以看出信竞队员的奇葩风气——还未学信竞的小朋友，慎入这个圈子！

在介绍莫队算法之前，先来看一道题：

给定一个长度为 $n$ 的序列和 $m$ 个形如 $(l,r)$ 的区间，求 $[l,r]$ 的区间和。

作为一道练手题，请使用莫队算法完成。

下面，我们用这道题来引入莫队算法的概念。

区间上的莫队算法

在了解算法之前，先明确一点：莫队算法就是优化的暴力。首先思考：如何用暴力解决这道题呢？只需要针对每个询问，计算累加和即可，时间复杂度是 $O(mn)$ 。

这样做，会造成大量的信息浪费。比如，前一个询问是 $(817,1926)$ ，后一个询问是 $(818,1989)$ ，如果两次都暴力累加，那么 $(818,1926)$ 的信息就会被浪费。根据区间和的性质，如果已知这两个询问，我们完全可以用 $(817,1926)$ 的结果减去 $(817,817)$ 的结果，再加上 $(1927,1989)$ 的结果。这样做，中间信息就会得到充分利用。这样做，很像螃蟹在数轴上爬：左右侧分开来算，螃蟹从第一个询问到第二个询问，总共只「爬」了 $(818-817)+(1989-1926)=64$ 步。

现在回到更一般的情形：如果我们面对一串随机询问，能否每次都照如上方式操作？再进一步，如果我们已知所有询问，如果求出一个合适的顺序，从而尽可能多地利用信息，说不定能达到「暴力出奇迹」的效果。

现在解决下一个问题：如何找到合适的顺序呢？有这样的一种方法：

让我们考察两个询问 $(x1,y1)$ 和 $(x2,y2)$ 。从第一个到第二个，螃蟹要「爬」 $abs(x1-x2)+abs(y1-y2)$ 步，每爬一步要用 $O(1)$ 的时间。这个形式让我们想到了什么？曼哈顿距离。我们要让螃蟹「爬」的次数尽可能少，因此，这个问题可以这样理解：把每个询问抽象成点 $(x,y)$ ，我们最终要求的是这些点的「曼哈顿距离最小生成树」，然后使用 DFS 进行转移。这样可以保证转移所花的时间最少。

不过，以上算法实现起来似乎十分复杂。放在这里，仅做拓展思路。我们来看看莫涛是怎么做的：

把数轴上的 $[1,n]$ 分成 $sqrt(n)$ 个块，每个块的长度为 $sqrt(n)$ 。
把所有询问 $(l,r)$ 以 $l$ 所在的块为第一关键字， $r$ 本身为第二关键字排序，然后按照上述方法进行处理。

可以看到，莫队算法是一种离线算法，必须读取所有询问后才能开始解决问题。按照这种方式排序，时间复杂度只有 $O(n·sqrt(n))$ ，是真真正正的「暴力出奇迹」。如何证明复杂度？

我们可以体会到，这种方法在移动左右区间上达到了一种微妙的「平衡」。下面是一个不太严格的证明：

对于右端点：
- 当左端点分块相同时，右端点最多变化 $n$ ，但分块只有 $sqrt(n)$ 个，所以复杂度为 $O(n·sqrt(n))$ 。
- 当左端点分块转移时，右端点最多变化 $n$ ，但分块只有 $sqrt(n)$ 个，所以复杂度也为 $O(n·sqrt(n))$ 。
对于左端点：
- 当分块相同时，左端点最多变化 $sqrt(n)$ 。
- 当分块转移时，左端点最多变化 $2sqrt(n)$ 。由于共有 $m$ 个询问，当 $m$ , $n$ 同阶，复杂度则为 $O(n·sqrt(n))$ 。

因此，总的时间复杂度为 $O(n·sqrt(n))$ 。

下面是代码：

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAX 100005
using namespace std;

int n, m, len, a[MAX], seq[MAX], dv[MAX], tmp,
    left, right, ans[MAX], l[MAX], r[MAX];

bool cmp(int a, int b) { // 以 l 所在的块为第一关键字，r 为第二关键字排序
  if (dv[l[a]] == dv[l[b]]) return r[a] < r[b];
  return dv[l[a]] < dv[l[b]];
}

int main()
{
  scanf("%d%d", &n, &m);  // n 是数列长度，m 是询问个数 
  for (int i = 1; i <= n; i++)
    scanf("%d", &a[i]); // 读入数列 
  len = sqrt(n);
  for (int i = 1; i <= n; i++)
    dv[i] = i / len; // dv[] 存储的是每个位置所在的块 
  for (int i = 1; i <= m; i++) {
    seq[i] = i;
    scanf("%d%d", &l[i], &r[i]);
  }
  sort(seq + 1, seq + m + 1, cmp);
  left = right = l[seq[1]];
  tmp = a[l[seq[1]]]; // 先计算出起始的位置
  for (int i = 1; i <= m; i++) {
    while (left < l[seq[i]]) tmp -= a[left++];
    while (left > l[seq[i]]) tmp += a[--left];
    while (right < r[seq[i]]) tmp += a[++right];
    while (right > r[seq[i]]) tmp -= a[right--]; // 在转移的时候要格外小心！ 
    ans[seq[i]] = tmp; // 由于不是按照原始顺序求解，必须把答案存下来，再按原始顺序输出 
  }
  for (int i = 1; i <= m; i++)
    printf("%d\n", ans[i]);
  return 0;
}

不过，既然我们有了 $O(nlogn)$ 的线段树，为什么非要用 $O(n·sqrt(n))$ 的莫队算法呢？

因为，使用线段树解决的问题必须满足「区间加和性质」——即为，两个相邻区间的答案可以直接相加。而有些不满足这些性质的问题，就只能靠莫队算法来帮忙了。

下面，我们来看一道不能用线段树解决的问题：

小 H 的项链 ——SDOI2009

有一个长度为 $n$ 的颜色序列。有 $m$ 个形如 $(l,r)$ 的询问，分别询问区间 $[l,r]$ 中有多少种不同的颜色。 $m<=200,000$ ，颜色种类 $<=1,000,000$ 。

很显然，颜色种数不能直接加和——我们必须考虑莫队算法。思考：已知 $[l,r]$ 区间的答案，如何推得 $[l,r+1]$ 的答案呢？

可以考虑定义一个记录颜色出现次数的数组。每次移动区间端点时，相应的颜色出现次数 $+1$ 或 $-1$ 。当某种颜色从无到有或从有到无时，更新计数器。该题可以用很多方法解决，但莫队算法是其中最简单的一种。

附上参考代码：

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 50004
#define MAXM 200005
using namespace std;

int m, n, dv[MAXM], seq[MAXM], l[MAXM], r[MAXM], a[MAXN];
int f[1000006], ans, left, right, res[MAXM];

bool cmp(int a, int b) {
  if (dv[l[a]] == dv[l[b]]) return r[a] < r[b];
  return dv[l[a]] < dv[l[b]];
}

int main()
{
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) {
    scanf("%d", &a[i]);
    dv[i] = (int)((double)i / (double)sqrt(n));
  }
  scanf("%d", &m);
  for (int i = 1; i <= m; i++) {
    seq[i] = i;
    scanf("%d%d", &l[i], &r[i]);
  }
  sort(seq + 1, seq + m + 1, cmp);
  for (int i = l[seq[1]]; i <= r[seq[1]]; i++) {
    if (!f[a[i]]) ans++;
    f[a[i]]++;
  }
  res[seq[1]] = ans;
  left = l[seq[1]];
  right = r[seq[1]];
  for (int i = 2; i <= m; i++) {
    while (left < l[seq[i]]) {
      f[a[left]]--;
      if (!f[a[left]]) ans--;
      left++;
    }
    while (left > l[seq[i]]) {
      left--;
      if (!f[a[left]]) ans++;
      f[a[left]]++;
    }
    while (right < r[seq[i]]) {
      right++;
      if (!f[a[right]]) ans++;
      f[a[right]]++;
    }
    while (right > r[seq[i]]) {
      f[a[right]]--;
      if (!f[a[right]]) ans--;
      right--;
    }
    res[seq[i]] = ans;
  }
  for (int i = 1; i <= m; i++)
    printf("%d\n", res[i]);
  return 0;
}

我们再来看一道区间上的莫队问题：

小 z 的袜子 ——2009 国家集训队

给定一个长度为 $n$ 的正整数列。有 $m$ 个形如 $(l,r)$ 的询问，分别询问在区间 $[l,r]$ 中任选两个数，相等的概率。用最简分数形式输出。

我们先用数学方式表达这个概率。容易知道，对于每个询问 $(l,r)$ ：

$P=sum(v,i=1)C(2,f(i))/C(2,d)$ 。

其中， $d=r-l+1$ （即区间宽度）， $v$ 表示数字的最大值， $f(x)$ 表示 $x$ 在该区间中的出现次数。

根据组合数公式 $C(n,m)=P(n,m)/m!=m!/(n!(m-n)!)$ 得 $C(2,m)=(m^2-m)/2$ 。因此上式可化为：

$P=sum(v,i=1)(f(i)^2)-sum(v,i=1)f(i)/(d^2-d)$ 。

根据表达式的意义，我们得知 $sum(v,i=1)f(i)=d$ 。故

$P=sum(v,i=1)(f(i)^2)-d/(d^2-d)$ 。

现在考虑：已知 $[l,r]$ 区间的答案，如何推得 $[l,r+1]$ 的答案？

对于所有和 $d$ 相关的部分，我们都可以方便地在 $O(1)$ 内求出新的值。
对于 $sum(v,i=1)(f(i)^2)$ ，我们需要用一个数组存下所有 $f(i)$ 的值。令要添加到区间内的数为 $z$ ，则只需减去 $f(z)^2$ ，把 $f(z)$ 的值 $+1$ ，然后把新的 $f(z)^2$ 加上去就行了。这个操作是 $O(1)$ 的。

同理，我们可以方便地从 $[l,r]$ 转移到 $[l,r-1]$ 、 $[l-1,r]$ 和 $[l+1,r]$ 。

于是，这个问题可以用莫队算法完美解决。

下面是最后一道区间莫队：

序列 ——来源：BZOJ

给定一个长度为 $n$ 的序列 $A$ 和 $q$ 个形如 $(l,r)$ 的询问。对于每个询问，求出 $[l,r]$ 内所有非空子串的最小数之和。

例如，对于序列 $5,2,4$ ，它的所有非空子串的最小数之和为 $5+2+4+2+2+2=17$ 。

$n,q<=100000$ 。

这也是典型的莫队算法的运用。按照惯例，我们思考：已知区间 $[l,r]$ 的答案，如何在 $O(1)$ 内求出 $[l,r+1]$ 的答案呢？

从 $[l,r]$ 到 $[l,r+1]$ ，实际上只多了以 $Ar+1$ 为结尾的 $(r-l+2)$ 个子串。定义 $f(l,r)$ 为以 $[l,r]$ 中的数为左端点的新子串对答案的贡献，则我们要求的是 $f(l,r+1)$ 。

我们可以使用 ST 表等工具在 $O(1)$ 内求出 $[l,r+1]$ 中最小元素的位置 $pos$ 。不难发现，以 $[l,pos]$ 为左端点的新子串中， $Apos$ 都是最小值。则 $f(l,pos)=Apos times (pos-l+1)$ 。于是问题转化为求 $f(pos+1,r+1)$ 。

为了方便，我们用 $left(x)$ 表示 $Ax$ 左边的第一个比它小的数的下标。换句话说，在区间 $[left(x)+1,x]$ 中，最小的数为 $Ax$ 。可以得到：

$f(pos+1,r+1)=A_{r+1}*(r+1-left(r+1))+f(pos+1,left(r+1))$ 。

同理，

$equation2$ 。

很显然，第二个参数每次取 $left$ ，它一定会取到这一段中最小值的下标 $pos$ 。此时，我们可以停止迭代。

于是，可以得到递推式：

$too-complicated$ 。

注意到：对于同样的 $r$ ，结果只与 $A$ 和终止位置 $pos$ 有关。不妨定义一个类似于前缀和的数组（本题下标从 $1$ 开始）：

$also-too-complicated$ 。

于是有

$f(pos+1,r+1)=g(r+1)-g(pos)$ 。

故

$answer$ 。

这也就是从 $[l,r]$ 转移到 $[l,r+1]$ ，需要加上的值。所有的操作都在 $O(1)$ 内。

按照同样的方法，可以从 $[l,r]$ 转移到 $[l,r-1]$ 、 $[l-1,r]$ 和 $[l+1,r]$ 。当然，这道题由于转换比较复杂，实现比较麻烦，大家可以自己思考。

如何找到 $left$ 数组？可以使用单调栈在 $O(n)$ 的时间内求出。具体算法如下：
1) 向栈内压入 0。
2) for i <– 1 to n:
a) 弹出栈顶所有大于 $Ai$ 的元素的下标。
b) left[i] <– 栈顶元素。
c) 向栈内压入 i。

莫队算法在树上的应用

实际上，莫队算法也是可以解决树上的区间问题的——只需稍加处理，就能用上面螃蟹「爬行」的思想解决这类问题。我们来看一个例子：

Count on a Tree Ⅱ ——来源：SPOJ

给一个树，树上的每个点都有颜色。有若干个形如 $(a,b)$ 的询问，求连接 $a$ 、 $b$ 两点的路径上的点有多少种颜色（包括端点）。

这和前面小 H 的项链有异曲同工之妙。如何将这个问题转化成普通的区间问题？很简单，通过 DFS 将树上的点拉成一个序列，即可进行操作。举一个例子：

tree

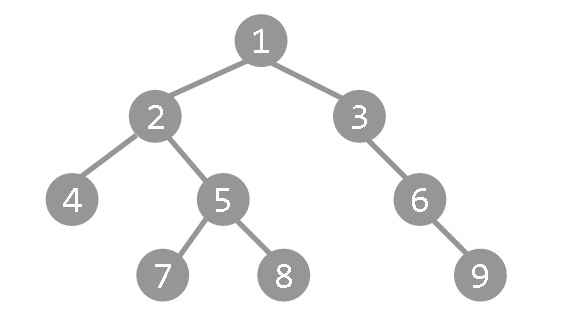
这是一个树。我们将树进行一次 DFS 遍历，当第一次到达和最后一次离开一个点时进行记录。对于上面的树，所得到的序列为：

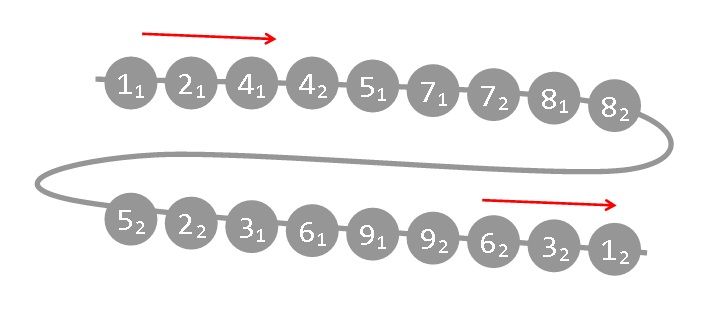
我们使用下标 1 表示第一次到达某点时的记录，下标 2 表示最后一次离开某点时的记录。

假如询问是 $[7,6]$ ，则不难发现：在用 DFS 得到的序列中找到 $72$ 和 $61$ ，则它们之间所有只出现一次的点，以及原树上它们的 LCA¹，即为原树中路径上的点（因为一个点出现两次相当于进入再离开，一定不是简单路径上的点）。

具体来讲，若给定两个点 $a$ 和 $b$ ：

若和的 LCA 是，则生成的序列形如：。原图中两点间的路径包括：
- 序列中 $a1$ 、 $b1$ 和它们之间的部分中只出现一次的点（取 $a2$ 、 $b2$ 也可以，其目的是不要重复计算 $a$ 或 $b$ ）；
若 $a$ 和 $b$ 的 LCA 是 $b$ ，情况与上类似；
若和的 LCA 是其它点，则序列形如。此时原图两点间的路径包括：
- 序列中 $a2$ 、 $b1$ 和它们之间的部分中只出现一次的点（目的同上）；
- $a$ 、 $b$ 的 LCA。

把每个询问都按如上方式对应到新生成的序列上，就可以使用莫队算法解决问题了。当然，这里的 LCA 最好使用离线的 Tarjan 算法求解，时间复杂度较低。（可以参阅这个博客了解 Tarjan 算法的具体操作。²）

在实现的时候要注意：区间内只出现一次的点才有效。所以，我们需要存下每个点当前在区间中出现了几次。如果新添加的点在区间中已出现 1 次，应该等同于删去它；如果要删去的点在区间中已出现 2 次，应该等同于添加它。另外，若 $a$ 和 $b$ 的 LCA 是其它点，别忘了在答案中加上 LCA 的贡献。除此之外，和普通的莫队算法没有区别。

我们来参观一下这道题的代码：

/* 代码有误，还通过不了原题，但意思可以参考…… */ 

#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAX 100005
using namespace std;

int n, m, ui, vi, qu[MAX], qv[MAX],
     squ[MAX], sqv[MAX], dv[MAX * 2], 
    rec[MAX], ans, left, right, f[MAX], clr[MAX], btw[MAX];
bool vst[MAX];

int w[MAX], c_w;
map<int, int> mp;
map<int, int>::iterator it;
void discrete(void);

struct info {
  int v, next;
} edge[MAX * 2];
int h_e[MAX], c_e;
void addEdge(int u, int v);

struct Query {
  int v, next, no;
} query[MAX * 2];
int h_q[MAX], c_q;
void addQuery(int u, int v, int no);

int qlca[MAX];
void get_lca(int tp);

int cnt, in[MAX], out[MAX], ontree[MAX], arr[MAX * 2];
void dfs(int tp, int fa);

int anc[MAX];
int find_anc(int x);

int seq[MAX * 2];
bool cmp(int a, int b);

int main()
{
  scanf("%d%d", &n, &m); // n 是点数，m 是询问个数
  for (int i = 1; i <= n; i++) // 读入点的权值
    scanf("%d", &w[i]);
  discrete();
  for (int i = 1; i <= n; i++)
    printf("%d ", w[i]);
  printf("\n");
  memset(h_e, -1, sizeof(h_e));
  for (int i = 1; i < n; i++) {  // 建树
    scanf("%d%d", &ui, &vi);
    addEdge(ui, vi);
    addEdge(vi, ui);
  }
  memset(h_q, -1, sizeof(h_q));
  for (int i = 1; i <= m; i++) {  // 读入询问，并用邻接链表处理
    scanf("%d%d", &qu[i], &qv[i]);
    addQuery(qu[i], qv[i], i);
    addQuery(qv[i], qu[i], i);
  } 
  for (int i = 1; i <= n; i++) // 初始化并查集
    anc[i] = i;
  get_lca(1); // 用 Tarjan 算法求出每个询问中两点的 LCA，保存在 qlca[] 中
  dfs(1, 1); // 将树转化成序列
  for (int i = 1; i <= m; i++) { // 将询问对应到序列上
    if (qlca[i] == qu[i] || qlca[i] == qv[i]) { // 如果两点的 LCA 是其中之一
      squ[i] = in[qu[i]];
      sqv[i] = out[qv[i]];
    }
    else {
      if (abs(out[qv[i]] - in[qu[i]]) > abs(in[qv[i]] - out[qu[i]])) {
        squ[i] = out[qu[i]]; // 通过比较大小确定前文中的 a_2 和 b_1
        sqv[i] = in[qv[i]];
      }
      else {
        squ[i] = in[qu[i]];
        sqv[i] = out[qv[i]];
      }
    }
    if (squ[i] > sqv[i]) swap(squ[i], sqv[i]);
  }
  for (int i = 1; i <= cnt; i++) {
    seq[i] = i;
    dv[i] = (int)((double)i / (double)sqrt(cnt)); // dv[] 存储的是序列上每个位置所在的块
  }
  sort(seq + 1, seq + cnt + 1, cmp);
  left = right = squ[seq[1]];
  f[arr[squ[seq[1]]]]++;
  btw[ontree[left]]++;
  ans = 1;
  for (int i = 1; i <= m; i++) { // 使用莫队算法转移 
    while (left < squ[seq[i]]) {
      f[arr[left]]--;
      btw[ontree[left]]--;
      if (!f[arr[left]]) {
        if (btw[ontree[left]] % 2 == 0) ans--;
        else ans++;
      }
      left++;
    }
    while (left > squ[seq[i]]) {
      left--;
      if (!f[arr[left]]) {
        if (btw[ontree[left]] % 2 == 0) ans++;
        else ans--;
      }
      f[arr[left]]++;
      btw[ontree[left]]++;
    }
    while (right < sqv[seq[i]]) {
      right++;
      if (!f[arr[right]]) {
        if (btw[ontree[right]] % 2 == 0) ans++;
        else ans--;
      }
      f[arr[right]]++;
      btw[ontree[right]]++; 
    }
    while (right > sqv[seq[i]]) {
      f[arr[right]]--;
      btw[ontree[right]]--;
      if (!f[arr[right]]) {
        if (btw[ontree[right]] % 2 == 0) ans--;
        else ans++;
      }
      right--;
    }
    rec[seq[i]] = ans;
    if (qlca[seq[i]] != qu[seq[i]] && qlca[seq[i]] != qv[seq[i]]) {
      if (!f[w[qlca[seq[i]]]]) 
        rec[seq[i]]++; // 算上 LCA 的贡献 
    }
  }
  for (int i = 1; i <= m; i++)
    printf("%d\n", rec[i]);
  return 0;
}
  
void discrete(void) { // 权值离散化 
  c_w = 1;
  for (int i = 1; i <= n; i++) {
    it = mp.find(w[i]);
    if (it == mp.end()) {
      mp[w[i]] = c_w++;
      w[i] = mp[w[i]];
    }
    else w[i] = mp[w[i]];
  }
}

void addEdge(int u, int v) {
  edge[c_e].v = v;
  edge[c_e].next = h_e[u];
  h_e[u] = c_e++;
}

void addQuery(int u, int v, int no) {
  query[c_q].v = v;
  query[c_q].no = no;
  query[c_q].next = h_q[u];
  h_q[u] = c_q++;
}

void dfs(int tp, int fa) { // 把树转换成序列 
  arr[++cnt] = w[tp];
  in[tp] = cnt;
  ontree[cnt] = tp;
  for (int i = h_e[tp]; i != -1; i = edge[i].next) {
    if (edge[i].v == fa) continue;
    dfs(edge[i].v, tp);
  }
  arr[++cnt] = w[tp];
  out[tp] = cnt;
  ontree[cnt] = tp;
}

void get_lca(int tp) { // 求出 LCA 
  anc[tp] = tp;
  vst[tp] = true;
  for (int i = h_e[tp]; i != -1; i = edge[i].next) {
    if (!vst[edge[i].v]) {
      get_lca(edge[i].v);
      anc[find_anc(edge[i].v)] = find_anc(tp);
    }
  }
  for (int i = h_q[tp]; i != -1; i = query[i].next) {
    if (vst[query[i].v])
      qlca[query[i].no] = find_anc(query[i].v);
  }
}

int find_anc(int x) {
  if (anc[x] == x) return x;
  return anc[x] = find_anc(anc[x]);
}

bool cmp(int a, int b) {
  if (dv[squ[a]] == dv[squ[b]])
    return sqv[a] < sqv[b];
  return dv[squ[a]] < dv[squ[b]];
}

需要注意的一点是，树上莫队算法还有直接在树上操作的实现，其中的分块和转移需要用到一些技巧。这篇博客比较深入地讲解了这种操作方式。

如果权值在边上呢？只需要把权值存在深度较大的点上即可。操作方式大同小异。

带修改的莫队算法

实际上，我们可以用莫队算法解决带修改的区间查询问题——只是较少使用。我们可以定义状态 $(l,r,t)$ 表示区间 $[l,r]$ 经过了 $t$ 次修改后的答案。把每个状态以 $l$ 所在分块为第一关键字、 $r$ 所在分块为第二关键字、 $t$ 本身为第三关键字排序。当每个分块的大小为 $n^(2/3)$ 时，时间复杂度可以达到 $O(n^(5/3))$ 。

相对来讲，带修改的莫队算法比较麻烦，这里就仅作介绍。

LCA：最近公共祖先。 ↩
请忽视该链接里满篇的英文拼写错误。 ↩

留下评论

注意评论系统在中国大陆加载不稳定。

imbiansl

莫队算法

区间上的莫队算法

莫队算法在树上的应用

带修改的莫队算法

分享

留下评论

猜你喜欢

Spark 0.5 关键组件与基本流程

【翻译】Lukas Dhont 专访

使用 Scrapy 搭建网络爬虫框架

Chapter 7: Runtime Environments