Hamilton 通路和回路的充分条件

对于图 \(G\)，若存在一条路径恰好经过每个顶点一次，该通路叫做 Hamilton 通路；若存在一条回路恰好经过每个顶点一次（始末点除外），该通路叫做 Hamilton 回路。

没有已知简单的充要条件可以判断 Hamilton 通路或回路是否存在，不过，人们发现，图 \(G\) 中的边数越多，就越可能存在 Hamilton 通路和回路。特别是，当图 \(G\) 已经存在 Hamilton 通路或回路时，若再向图中加新的边（但不增加顶点），新图中依然存在 Hamilton 通路或回路。我们有理由认为，当图中顶点的度数充分大时，Hamilton 通路或回路一定存在。本文将介绍并证明几个和顶点度数相关的充分条件。

Hamilton 通路存在的充分条件

定理：令 \(G=(V,E)\) 为简单图，其中 \(|V| = n \geq 3\)。若对于每一对不相邻的顶点 \((u,v)\)，都有 \(\deg(u) + \deg(v) \geq n - 1\)，则 \(G\) 中存在 Hamilton 通路。

证明：首先证明 \(G\) 是连通图。若 \(G\) 不连通，令 \(C_1\)、\(C_2\) 为 \(G\) 的其中两个连通分量，分别有 \(n_1\)、\(n_2\) 个顶点。令 \(u\) 是 \(C_1\) 中的顶点，\(v\) 是 \(C_2\) 中的顶点。由于 \(G\) 是简单图，\(C_1\)、\(C_2\) 也是简单图，即无重边、无环。则有

\[\begin{align} \deg(u) \leq n_1 - 1\\\deg(v) \leq n_2 - 1\\ \end{align}\]

两式相加，得：

\[\begin{align} \deg(u) + \deg(v) \leq n_1 + n_2 - 2 \leq n - 2\\ \end{align}\]

这与已知条件矛盾。因此 \(G\) 必定连通。

下面，我们要在连通图 \(G\) 中构造出一条 Hamilton 通路。先约定记号 \(p_m\) 为长度为 \(m - 1\) 的简单路径（无重复顶点）\(\{v_1, v_2\}\), \(\{v_2, v_3\}\), \(\ldots\), \(\{v_{m-1}, v_m\}\) \((m \geq 2)\)。\(p_2\) 必定存在，因为 \(G\) 连通，即任意顶点 \(v_1\) 都与至少一个其他顶点 \(v_2\) 与之相连，取路径 \(\{v_1, v_2\}\) 作为 \(p_2\) 即可。\(p_n\) 即为我们要找的 Hamilton 通路。现在我们需要证明，对于任意简单路径 \(p_m (2 \leq m \leq n - 1)\)，都有办法将其扩展为更长的路径，直到找到 \(p_n\) 为止。我们分以下几种情况讨论。

1. \(v_1\) 或 \(v_m\) 与 \(p_m\) 外的任一顶点相邻。假设 \(v_1\) 与 \(p_m\) 外的顶点 \(v\) 相邻，则只需将边 \(\{v_1, v\}\) 并入 \(p_m\)，再将所有顶点重新标号，即可得到 \(p_{m+1}\)。若是 \(v_m\) 与 \(v\) 相邻，同理。

2. \(v_1\) 和 \(v_m\) 都只与 \(p_m\) 内的顶点相邻。下面会证明，在这种情况下，\(p_m\) 中的所有顶点一定组成一条简单回路（无重复顶点）。先约定记号 \(S\) 为 \(p_m\) 中与 \(v_1\) 相邻的所有顶点组成的集合，\(\lvert S\rvert = k\)。

• 若 \(\exists v_t \in S\)，使得 \(v_{t-1}\) 与 \(v_m\) 相邻，我们只需添加边 \(\{v_1, v_t\}\) 和 \(\{v_{t-1}, v_m\}\)，再删除边 \(\{v_{t-1}, v_t\}\) 即可得到由 \(p_m\) 的所有顶点组成的简单回路，如下图所示。（该情况包含了 \(v_1\) 与 \(v_m\) 相邻的情形。）

• 若 \(!\exists v_t \in S\)，使得 \(v_{t-1}\) 与 \(v_m\) 相邻，则在 \(\{v_1, v_2, \ldots, v_{m-1}\}\) 中，至少有 \(k\) 个顶点不与 \(v_m\) 相邻。又因为 \(v_m\) 只与 \(p_m\) 内的顶点相邻，所以 \(\deg(v_m) \leq m - 1 - k\)。又因为 \(\deg(v_1) = k\)，两式相加，得到 \(\deg(v_1) + \deg(v_m) \leq m - 1 < n - 1\)，这与已知条件矛盾。所以该情况不存在。

现在我们证明了 \(p_m\) 中的所有顶点形成简单回路。任取 \(p_m\) 之外的任意顶点 \(v\)，由图的连通性，一定存在一条连接 \(v\) 和 \(p_m\) 上某顶点 \(v_r\) 的路径。将该路径中所有边添加进 \(p_m\)，删掉原回路中任一条以 \(v_r\) 为端点的边，再将所有顶点重新标号，即可得到 \(p_{m+l}\)，\(l\) 为 \(v\) 到 \(p_m\) 的最短距离，如下图。

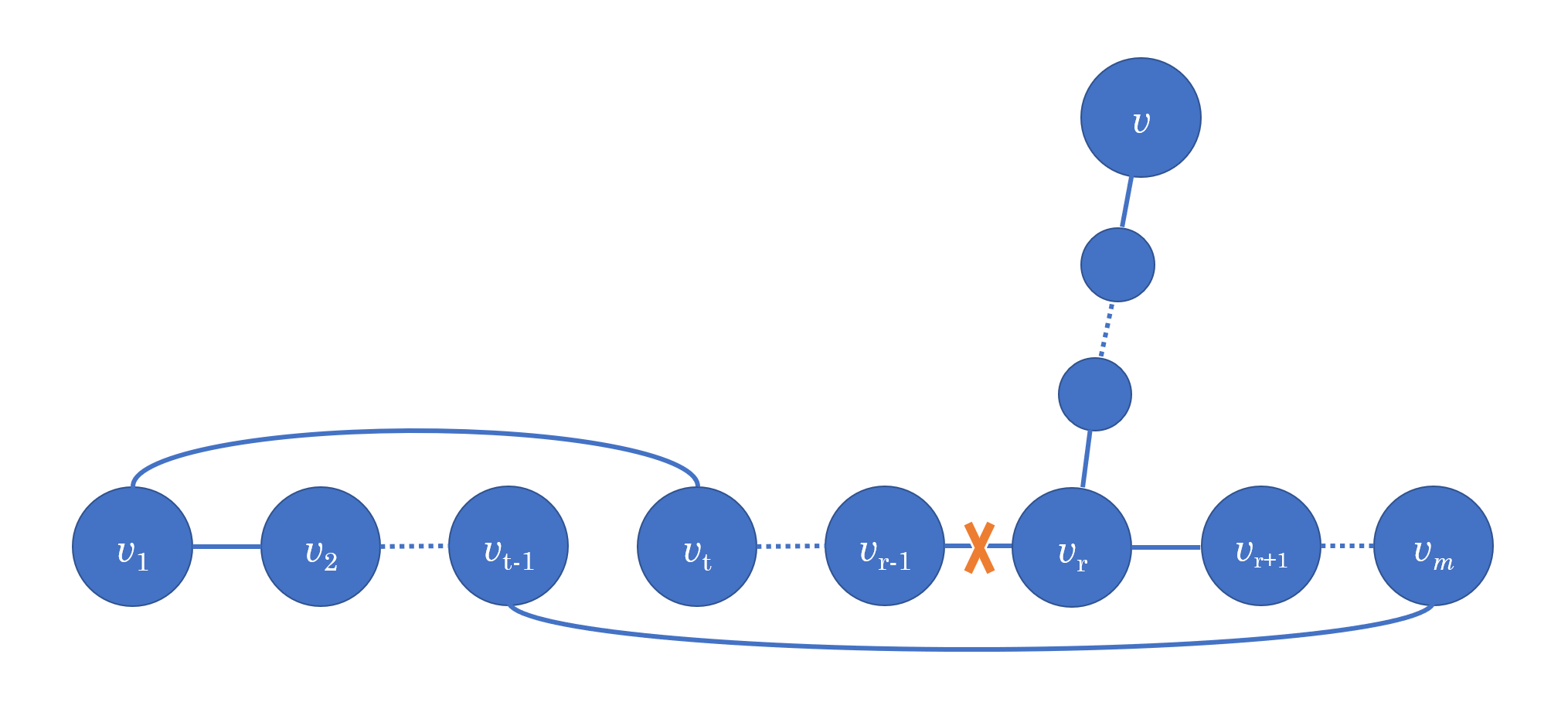
综合 1、2 两种情况，我们证得，对于任意路径 \(p_m (2 \leq m \leq n - 1)\)，都有办法将其扩展为更长的路径，直到找到 \(p_n\)。因此 Hamilton 通路存在。∎

Hamilton 回路存在的充分条件

Ore 定理

令 \(G=(V,E)\) 为简单图，其中 \(|V| = n \geq 3\)。若对于每一对不相邻的顶点 \((u,v)\)，都有 \(\deg(u) + \deg(v) \geq n\)，则 \(G\) 中存在 Hamilton 回路。

证明：该定理实际上是增强了上节定理中的条件。我们直接利用上节中的定理来证明。

由于 \(\deg(u) + \deg(v) \geq n > n - 1\)，所以 \(\deg(u) + \deg(v) \geq n - 1\)。由上节定理，我们可以直接证得图 \(G\) 中存在 Hamilton 通路 \(p_n\)。现在，我们用类似上节中第二种情况的方法，证明 \(p_n\) 中的所有顶点可以构成 Hamilton 回路。先约定记号 \(S\) 为 \(p_n\) 中与 \(v_1\) 相邻的所有顶点组成的集合，\(\lvert S\rvert = k\)。

• 若 \(\exists v_t \in S\)，使得 \(v_{t-1}\) 与 \(v_n\) 相邻，我们只需添加边 \(\{v_1, v_t\}\) 和 \(\{v_{t-1}, v_n\}\)，再删除边 \(\{v_{t-1}, v_t\}\) 即可得到由 \(p_n\) 的所有顶点组成的简单回路。（该情况包含了 \(v_1\) 与 \(v_n\) 相邻的情形。）

• 若 \(!\exists v_t \in S\)，使得 \(v_{t-1}\) 与 \(v_n\) 相邻，则在 \(\{v_1, v_2, \ldots, v_{n-1}\}\) 中，至少有 \(k\) 个顶点不与 \(v_n\) 相邻，所以 \(\deg(v_n) \leq n - 1 - k\)。又因为 \(\deg(v_1) = k\)，两式相加，得到 \(\deg(v_1) + \deg(v_n) \leq n - 1\)，这与已知条件矛盾。所以该情况不存在。

综上，\(p_n\) 中的所有顶点可以构成 Hamilton 回路。Hamilton 回路存在。∎

Dirac 定理

令 \(G=(V,E)\) 为简单图，其中 \(|V| = n \geq 3\)。若对于任一顶点 \(u\)，都有 \(\deg(u) \geq \lceil \frac{n}{2} \rceil\)，则 \(G\) 中存在 Hamilton 回路。

证明：该定理条件蕴含了 Ore 定理的条件，由 Ore 定理成立，得 Dirac 定理成立。∎