Chapter 2: Scanning

2.1 The Scanning Process

Tokens: The logical units the scanner generates, which are dealt with by further parts of the compiler (usually the parser).

Categories of tokens:

• Reserved words
• Special symbols
• Numbers and identifiers

The string of characters represented by a token is called its string value or lexeme. Reserved words have one lexeme (e.g. IF has only one lexeme if). Identifiers are infinite, but they share the same token ID.

Any value associated to a token is called an attribute to the token, This can be a string value, or a numeric value computed from the string content. For example, a NUM can have a string value 32767, or a numeric value of the number 32767 (in which case the string value can be safely discarded).

In C, we can define a token record:

typedef struct {
  TokenType tokenval;
  union {
    char* stringval;
    int numval;
  } attribute;
} TokenRecord;

And a C function:

TokenType getToken(void);

The function will return the next token from the input, as well as compute additional attributes. The input string is managed by system input facilities.

2.2 Regular Expressions

A regular string \(r\) is defined by the set of strings it matches. The set is called the language generated by the regular expression, written as \(L(r)\).

• Symbols: the set of characters a language uses. The set of legal symbols is called the alphabet and written as \(\Sigma\).
• A character written in boldface indicates a pattern.
• Metacharacters in a regular expression (*, +, etc.) have special meanings.

2.2.1 Definition of Regular Expressions

Basic regex:

• Any character \(a\) from the alphabet \(\Sigma\) stands for itself. e.g. \(L(\mathbf{a}) = \{a\}\)
• Empty string: \(L(\mathbf{\epsilon})=\{\epsilon\}\)
• Empty set: \(L(\emptyset)=\{\}\)

Regex operations:

• Choice among alternatives: \(L(r\vert s)=L(r)\cup L(s)\)
• Concatenation: \(L(ab)=L(a)L(b)\)
• Repetition (Kleene closure): Define an operation \(S*=\{\epsilon\}\cup S \cup SS \cup SSS \cup \dots\). Then \(L(r*)=L(r)*\)

Precedence: repetition > concatenation > choice. Use parentheses to indicate a different precedence.

Extensions to regex:

• One or more repetitions: \(r+\) means \(rr*\)
• Any character: use a period \(.\)
• A range of characters: \([0-9]\) for \((0\vert 1\vert \dots\vert 9)\), \([abc]\) for \((a\vert b\vert c)\), \([A-Za-z]\) for any lowercase or uppercase letter.
• Any character not in a given set: \(\sim(a\vert b\vert c)\) for a character that is not either a or b or c.
  • Alternative symbol: \([\wedge abc]\) for a character that is not either a or b or c.
• Optional subexpressions: e.g. \((+\vert -)?[0-9]+\) for signed or natural numbers.

Regular expression cannot count. For example, \(S = \{b, aba, aabaa, aaabaaa, \dots \}\) cannot be described in regex.

A set of strings that is the language for a regex is called a regular set.

Problems in using regex for programming language tokens:

• Ambiguity: some strings can be matched by different regexes. We need to give disambiguating rules for these cases. For example:
  • Reverse words have a higher precedence than identifiers
  • When a string can be a single token or a sequence of several tokens, the single-token interpretation is preferred (principle of longest substring)
• Delimiters: characters that are unambiguously part of other tokens, e.g. newline, blank, tab or comment.
• Delimiters end token strings but they are not part of the token itself. This involves lookahead. The delimiter read should be returned back to the input string, or a lookahead is performed before removing the character from the input.

2.3 Finite Automata

• Circles are states
  • Circles with double borders are accepting states
• Arrow are state transitions

2.3.1 Definition of Deterministic Finite Automata

Deterministic finite automata (DFA): automata where the next state is unique given by the current state and the current input character.

Formal definition:

2.3.2 Lookahead, Backtracking, and Nondeterministic Automata

What the DFA diagram does not specify:

• Error transitions, and what happens when an error occurs (back up in the input, i.e., backtrack, or generate an error token)
• What happens when matching a character (usually moving the character from the input string to the token’s buffer)
• What happens when reaching an accepting state (returning the recognised token along with associated attributes)

e.g. The finite automata for recognising an identifier:

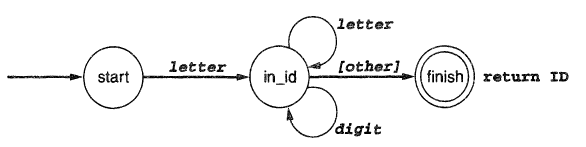
The square brackets around other indicates that the delimiting character should be considered lookahead, that is, that is should be put back to the input string.

ε-transition: a transition that may occur without consulting the input string (and without consuming any character).

Nondeterministic Finite Automata: a generalized form of finite automata where more than one transition from a state may exist for a particular character.

Formal definition:

2.3.3 Implementation of Finite Automata in Code

To simulate a DFA:

• Use position in the code to maintain the state implicitly

• Use a variable to maintain the current state and write transitions as a doubly nested case statement inside a loop

  state = 1
  while state not in accepting_states:
    match state:
      case 1:
        # operations
        state = x
      case 2:
        # operations
        state = y
      ...
  if state == 3:
    accept()
  else:
    error()
  

• Use a transition table (2D array) indexed by state and input character that expresses the values of the transition function T(state, character).

  • Accept[state] is a bool array indicating if the state is an accepting state.

  • Advance[state, ch] is a bool array indicating whether the transition will advance the input.

  • The code scheme applies to any transition table (table-driven):

    state = 1
    ch = next_input_character()
    while not Accept[state] and not error(state):
      newstate = T[state, ch]
      if Advance[state, ch]:
        ch = next_input_character()
      state = newstate
    if Accept[state]:
      accept()
    

• NFAs can be implemented in similar ways, but there are multiple choices in some states. A program will have to store up transitions and backtrack on failure. We prefer to convert the NFA to a DFA.

2.4 From Regex to DFAs

Regex → NFA → DFA → program

2.4.1 Regex to NFA: Thompson’s Construction

Basic regex:

• \(\mathbf{a}\):

  

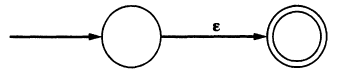
• \(\epsilon\):

  

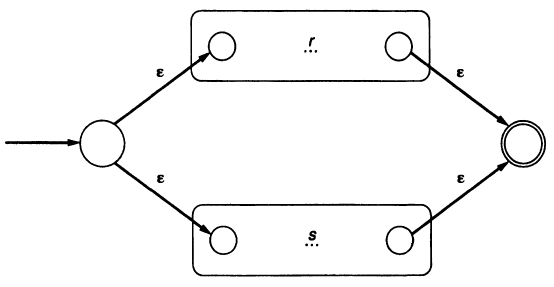
Concatenation: connect the accepting state of r to the start state of s by an ε-transition. \(rs\)

Choice: \(r\vert s\)

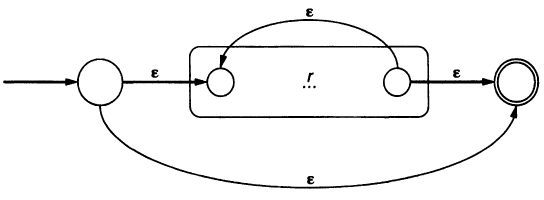
Repetition: \(r*\)

2.4.2 From an NFA to a DFA: Subset Construction

ε-closure: The ε-closure of a single state \(s\) is the set of states reachable by a series of zero or more ε-transitions, written as \(\bar{s}\). The ε-closure of a state always contains the state itself。

The ε-closure of a set of states is the union of the ε-closures of each individual state.

The subset construction: We would like to construct a DFA from a given NFA \(M\), which we call \(\overline{M}\).

• First, compute the ε-closure of the start state of \(M\). This becomes the start state of \(\overline{M}\).
• For this set and for each subsequent set \(S\), compute the transitions on characters \(a\) as follows:
  • Compute the state \(S_a' = \{t\vert \text{for some }s\text{ in }S\text{ there is a transition from }s\text{ to }t\text{ on }a\}\).
  • Compute \(\overline{S_a'}\). This defines a new state with a new transition \(S\xrightarrow{a}\overline{S_a'}\). Mark the state \(\overline{S_a'}\) as an accepting state if it contains an accepting state of \(M\).
  • Continue this process until no new states or new transitions are created.

For examples, see P70.

2.4.4 Minimizing the Number of States in a DFA

In automata theory, given any DFA, there is an equivalent DFA containing a minimum number of states, and this minimum-state DFA is unique.

The algorithm:

• Make the most optimistic assumption: only two sets, on consisting of all the accepting states, the other consisting of other states.
• Consider the transitions on each character \(a\) on the original DFA. For each set:
  • If all states in the set have transitions on \(a\) to all states in the set, define an \(a\)-transition from the new state to itself.
  • If two states \(s\) and \(t\) in the set have transitions on \(a\) that land in different sets, we say \(a\) distinguishes the states \(s\) and \(t\). The set has to be split according to where the transitions land.
• Repeat this process until either all sets contain only one element or until no further splitting of sets occurs.

Note that error transitions have to be taken into account, because an error state is nonaccepting. If there are states \(s\) and \(t\) from the same set such that \(s\) has an \(a\)-transition to another accepting state, while \(t\) has no \(a\)-transition at all (i.e., an error transition), then \(a\) distinguishes \(s\) and \(t\).