Chapter 3: Context-Free Grammars and Parsing

Parsing: determine the syntax/structure of a program. The result is a parse tree or syntax tree.

The major difference between a context-free grammar and regular expressions: Context-free grammar are recursive. (This allows if statements to be nested, for example.)

Two categories of algorithms for parsing: top-down and bottom-up.

3.1 The Parsing Process

Input: sequence of tokens. Output: syntax tree. The sequence of tokens is provided by the scanner as needed. In a single-pass compiler, the parser will directly output the target code, and the syntax tree is generated implicitly.

It’s more difficult for the parser to handle errors than the scanner. The scanner usually passes the error to the parser by generating an error token. The parser must report the error message, recover from the error and continue parsing (to find as many errors as possible).

3.2 Context-Free Grammars

Example: simple integer arithmetic operations.

exp -> exp op exp | ( exp ) | number
op -> + | - | *

3.2.1 Comparison to Regular Expression Notation

• No meta-symbol for repetition (*).
• Use arrow symbol (->) to express the definitions of names.
• Grammar rules like above are said to be in Backus-Naur Form (BNF).

3.2.2 Specification of Context-Free Grammar Rules

• The first symbol is a name for a structure.

• The second symbol is ->.

• Then follows a string of symbols, each of which is either a symbol from the alphabet (if / then / + / := / …), a name for a structure, or |.

• Sometimes we surround structure names with angle brackets (<...>) and write token names in uppercase. For example,

  <exp> ::= <exp> <op> <exp> | (<exp>) | NUMBER
  <op> ::= + | - | *
  

3.2.3 Derivations and the Language Defined by a Grammar

A derivation is a sequence of replacements of structure names by choices on the right-hand sides of grammar rules. The set of all strings of token symbols obtained by derivations from the exp symbol is the language defined by the grammar of expressions. i.e. \(L(G) = \{ s \vert exp \Rightarrow* s\}\)

For example, how to derive (34 - 3) * 42 from the grammar above:

exp => exp op exp
    => exp * NUMBER
    => ( exp ) * NUMBER
    => ( exp op exp ) * NUMBER
    => ( NUMBER - NUMBER ) * NUMBER

• The start symbol is the first symbol of the first rule. It is the most general structure of a program.

• Structure names are called nonterminals, since they must be replaced further on. Symbols in the alphabet are called terminals, since they terminate a derivation.

• Repetition can be achieved by recursion. For example, a+ can be written by:

  A -> A a | a  // Left recursive
  

  or

  A => a A | a  // Right recursive
  

3.3 Parse Trees and Abstract Syntax Trees

3.3.1 Parse Trees

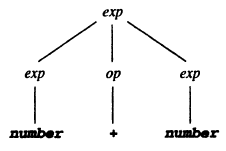
The parse tree for the derivation:

exp => exp op exp
    => NUMBER op exp
    => NUMBER + exp
    => NUMBER + NUMBER

• Left-most derivation: a derivation in which the leftmost nonterminal is replaced at each step in the derivation. Corresponds to a pre-order traversal of the parse tree.
• Right-most derivation: ditto. Corresponds to the reverse of a post-order traversal of the parse tree.

3.3.2 Abstract Syntax Trees

The principle of syntax-directed translation: the meaning, or semantics, of the string should be directly related to its syntactic structure as represented by the parse tree. The parse tree above contained the same information as below, which is known as an [abstract] syntax tree:

The token sequence cannot be recovered, unlike parse trees.

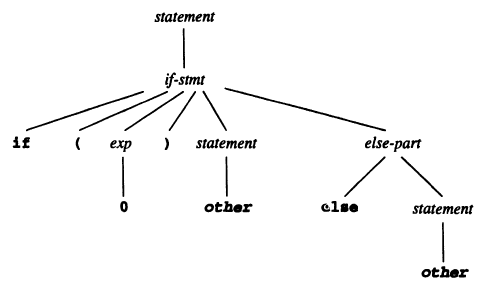
e.g. Consider the if statement if (0) other else other. The grammar:

statement -> if-stmt | OTHER
if-stmt -> IF ( exp ) statement else-part
else-part -> ELSE statement | ε
exp -> 0 | 1

The parse tree:

The corresponding syntax tree:

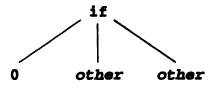
e.g. The grammar for a sequence of statement:

stmt-sequence -> stmt ; stmt-sequence | stmt
stmt -> s

s ; s ; s can be presented by this simplified syntax tree:

s -- s -- s

3.4 Ambiguity

3.4.1 Ambiguous Grammars

Ambiguous grammar: that generates a string with two distinct parse trees.

There is no algorithm to remove ambiguity in grammars. It should be avoided manually by:

• A disambiguating rule: state a rule that specifies in each ambiguous case which parse tree to use. (e.g. precedence, associativity)
• Change the grammar to eliminate ambiguity. (e.g. specify a grammar in which associativity is not allowed, only fully parenthesized expressions)

3.4.2 Precedence and Associativity

Replace

exp -> exp addop exp | term

by

exp -> exp addop term | term // left associative, or
exp -> term addop exp | term

3.4.3 The Dangling Else Problem

Consider

statement -> if-stmt | OTHER
if-stmt -> IF ( exp ) statement
           | IF ( exp ) statement ELSE statement
exp -> 0 | 1

IF ( 0 ) IF ( 1 ) OTHER ELSE OTHER

The ELSE statement can be associated to the first or second IF statement. To enforce the most closely nested rule, we can add a disambiguating rule, or change the grammar to:

statement -> matched-stmt | unmatched-stmt
matched-stmt -> IF ( exp ) matched-stmt ELSE matched-stmt | OTHER
unmatched-stmt -> IF ( exp ) statement
                  | IF ( exp ) matched-stmt ELSE unmatched-stmt
exp -> 0 | 1

In this way, only a matched statement can appear before ELSE, forcing else-parts to be matched as soon as possible.

Or, we could use a bracketing keyword like end if for the if statement. The corresponding grammar is:

if-stmt -> IF condition THEN statement-sequence END IF
           | IF condition THEN statement-sequence
                          ELSE statement-sequence END IF

3.4.4 Inessential Ambiguity

When a grammar produces distinct syntax trees which represent the same semantic value, the ambiguity is inessential.

3.5 Extended Notations: EBNF and Syntax Diagrams

3.5.1 EBNF Notation

EBNF: Extended BNF.

Repetition: use { ... } . e.g. A -> β { α }

• Note that when the associativity matters, A -> b { x b } implies left associativity, while right associativity is represented using optional parts.

Optional: use [ ... ].

• Right associativity: A -> b [ x A ]