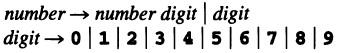Chapter 6: Semantic Analysis

Semantic analysis: the phase of the compiler that computes additional information needed for compilation once the syntactic structure of a program is known. It involves computing information beyond the capabilities of context-free grammars (beyond the syntax).

Semantic analysis includes: building a symbol table, performing type inference, and type checking.

Semantic analysis can be divided into:

• Checking the program to establish its correctness and to guarantee proper execution. (This chapter)
• Analysing the program to enhance the efficiency of execution of the translated program, done by compilers. (Next chapter)

6.1 Attributes and Attribute Grammars

Attributes: any property of a programming language construct, including:

• The data type of a variable
• The value of an expression
• The location of a variable in memory
• The object code of a procedure

Attributes may be fixed before compilation (e.g. the number of significant digits in a number), determined during compilation, or only determinable during program execution. The process of computing an attribute and associating the value with the language construct is called the binding of that attribute.

Attributes that can be bound prior to execution are static; attributes that can only be bound during execution are dynamic.

Attribute computations can take place in scanning, parsing and code generation. We focus on computations that happen before code generation and after parsing.

6.1.1 Attribute Grammars

Syntax-directed semantics: attributes are directly associated with grammar symbols. If \(X\) is a grammar symbol, and \(a\) is an attribute associated with \(X\), \(X.a\) means the value of \(a\) associated to \(X\).

For each grammar rule \(X_0 \rightarrow X_1 X_2 \dots X_n\) where \(X_0\) is a terminal and other \(X_i\) are arbitrary symbols, there is an attribute equation or semantic rule for each i and j:

\[X_i.a_j=f_{ij}(X_0.a_1,\dots,X_0.a_k,X_1.a_1,\dots,X_1,a_k,\dots,X_na_1,\dots,X_n.a_k)\]

An attribute grammar is the collection of all such equations.

Typically attribute grammars are simple and written in tabular form.

Example: for the grammar for unsigned numbers:

The grammar rule for the val attributes that contain the actual value of each symbol:

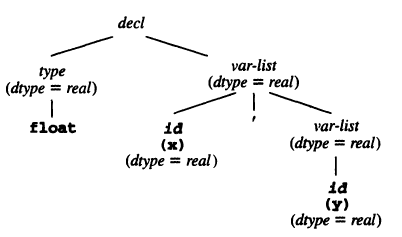
Example: consider the grammar for variable declarations:

decl -> type var_list
type -> INT | FLOAT
var_list -> ID, var_list | ID

The attribute grammar:

We can attach attribute equations to the nodes in the parse tree for float x,y:

Attribute grammars can declare error that cannot be conveniently expressed in grammar rules.

6.1.2 Simplifications and Extensions to Attribute Grammars

• Predefined functions, e.g. int numval(char D)
• Use an ambiguous but simpler form of the original grammar, because ambiguity has already been dealt with at the parsing stage.
• Use an abstract syntax tree instead of a parse tree.

Is it not yet possible to determine if a particular attribute grammar is consistent and complete (uniquely defines the given attributes). It is the algorithms for computing attributes that determine whether an attribute grammar is adequate.

6.2 Algorithms for Attribute Computation

Attribute equations cannot have circular dependencies. We need to find an order for the attributes that will ensure that all attribute values used in each computation are available when each computation is performed.

6.2.1 Dependency Graphs and Evaluation Order

Each grammar rule choice has an associated dependency graph. For each i, j, m and k in each attribute equation

\[X_i.a_j=f_{ij}(\dots,X_m.a_k,\dots)\]

the dependency graph contains an edge from the node \(X_m.a_k\) to the node \(X_i.a_j\). The nodes associated with each symbol \(X\) are drawn in a group. The dependency graph is usually drawn alongside the parse tree. For example, the dependency graph for float x,y:

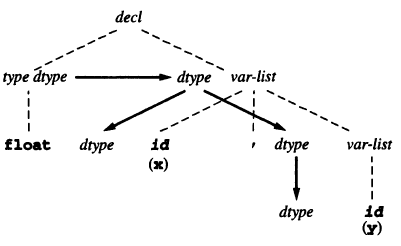
The dependency graph has to be a directed acyclic graph (DAG) to avoid circular dependencies.

Note that the attribute values on the roots of the DAG have to be ready prior to the computation. They are usually provided by the scanner or the parser.

How do we determine the order for attribute computation?

• Parse tree method: construct the dependency graph based on the specific parse tree at compile time. This adds complexity and requires the detection of circular dependencies.
• Rule-based method: Instead, the compiler writer analyses the attribute grammar and fixes an order for attribute evaluation at compiler construction time.

The set of attribute grammars to which this is applicable is a subset of all noncircular attribute grammars, hence are called strongly noncircular attribute grammars.

6.2.2 Synthesized and Inherited Attributes

Definitions:

• An attribute is synthesized if all its dependencies point from child to parent in the parse tree. An attribute grammar in which all the attributes are synthesized is called an S-attributed grammar.
• An attribute that is not synthesized is called an inherited attribute. They have dependencies that flow either from parent to children or from sibling to sibling. The latter case is classified as inherited because sibling inheritance is often implemented in such a way that the attribute is passed to the sibling via the parent.

The attribute values of an S-attributed grammar can be computed by a single bottom-up, or postorder, traversal of the parse tree. The order for inherited attributes, however, has to be carefully designated.

6.2.3 Attributes as Parameters and Returned Values

Sometimes we do not need to store attributes inside nodes of the parse tree. We can pass the inherited attribute values as parameters to recursive calls and receive synthesized attribute values as returned values of those same calls.

6.2.4 The Use of External Data Structures to Store Attribute Values

Data structures such as lookup tables, graphs and other structures may be useful to obtain the correct behaviour and accessibility of attribute values. The attribute grammar can be modified to reflect this need by replacing attribute equations (which are assignments) by calls to procedures representing operations on external data structures.

6.2.5 The Computation of Attributes During Parsing

Historically, there is an emphasis on performing attribute computation in one pass.

Which attributes can be successfully computed during a parse depends on the properties of the parsing method. In typically parsing algorithms, the input is read from left to right. This is equivalent to a left-to-right traversal of the parse tree. For synthesized attributes, this is not a problem, but for inherited attributes, this means no “backword” dependencies are allowed. Grammars that satisfy this are called L-attributed.

Formally:

An attribute grammar for attributes \(a_1, \dots, a_k\) is L-attributed if, for each inherited attribute \(a_j\) and each grammar rule \(X_0 \rightarrow X_1 X_2 \dots X_n\), the associated equations for \(a_j\) are all of the form

\[X_i.a_j=f_{ij}(X_0.a_1,\dots,X_0.a_k,X_1.a_1,\dots,X_1.a_k,\dots,X_{i-1}.a_1,\dots,X_{i-1}.a_k)\]

That is, the value of \(a_j\) at \(X_i\) can only depend on the attributes of the symbols \(X_0, \dots, X_{i-1}\) that occur to the left of \(X_i\) in the grammar rule.

An S-attributed grammar is L-attributed.

Computing Attributes During LR Parsing

• Use a value stack to store synthesized attributes. The value stack is manipulated in parallel with the parsing stack.
• Suppose the grammar is L-attributed, then inherited values of a token only depend on the previous tokens. The value of an inherited value can be stored in a variable prior to the recognition of the token by introducing an ε-production before the recognition of the token that schedules the storing of the top of the value stack.
• Alternatively, previous synthesized values can be accessed directly on the value stack.

6.2.6 The Dependence of Attribute Computation of the Syntax

Given an attribute grammar, all inherited attributes can be changed into synthesized attributes by suitable modification of the grammar, without changing the language of the grammar.